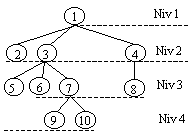
Definitia 1: Se numeste Arbore cu rădacină = graf neorientat conex fără cicluri în care unul din noduri este desemnat ca rădăcină. Nodurile pot fi aşezate pe niveluri începând cu rădăcina care este plasată pe nivelul 1.
Rădăcină = Nod special care generează aşezarea unui arbore pe niveluri; Această operaţie se efectuează în funcţie de lungimea lanţurilor prin care celelalte noduri sunt legate de rădăcină.
Descendent = într-un arbore cu rădăcină nodul y este descendentul nodului x dacă este situat pe un nivel mai mare decât nivelul lui x şi există un lanţ care le uneşte şi nu trece prin rădăcină.
Descendent direct / fiu = într-un arbore cu rădăcină nodul y este fiul (descendentul direct) nodului x dacă este situat pe nivelul imediat următor nivelului lui x şi există muchie între x şi y.
Ascendent = într-un arbore cu rădăcină nodul x este ascendentul nodului y dacă este situat pe un nivel mai mic decât nivelul lui y şi există un lanţ care le uneşte şi nu trece prin rădăcină.
Ascendent direct / părinte= într-un arbore cu rădăcină nodul x este părintele (ascendentul direct) nodului y dacă este situat pe nivelul imediat superior (cu număr de ordine mai mic) nivelului lui y şi există muchie între x şi y.
Fraţi = într-un arbore cu rădăcină nodul x este fratele nodului y dacă au acelaşi părinte.
Frunză = într-un arbore cu rădăcină nodul x este frunză dacă nu are nici un descendent direct
|
Arbore cu rădăcină
|
- Nodul 1 este rădăcină.
- Nodurile 5, 6, 7 sunt fii nodului 3.
- Nodul 7 este părintele nodurilor 9 şi 10;
- Nodul 9 este descendentul lui 3
- Nodul 3 este ascendentul lui 10
- Nodurile 8, 9 şi 10 sunt frunze
- Nodurile 5, 6 şi 7 sunt fraţi.
|
METODE DE MEMORARE A ARBORILOR
Cum un arbore este un caz particular de graf neorientat inseamna ca poate fi reprezentat ca un graf. De aici rezulta ca pentru reprezentarea unui arbore se pot utiliza:
1. Metode specifice grafurilor:
-matricea de adiacenta
-liste de adiacente
2. Metode specifice arborilor:
-prin legaturi de tip TATA. Arborele se reprezinta sub forma unui vector t cu n componente (n reprezinta numarul de noduri). Daca t[i]=k atunci nodul I este descendent al nodului k. Daca nodul I este varf atunci t[i]=0.
Fie arboreal din figura:
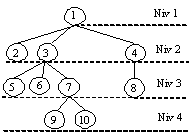unde nodul 1 este radacina. Atunci vectorul de tip tata este:
Legatura de tip TATA se mai numeste si legatura cu referinte ascendente.
Legatura de tip TATA este determinata si de modul in care am ales nodul radacina. Spre exemplu daca vom considera nodul 4 ca fiind radacina vom obtine o alta solutie.
Definim nivelul unui nod, recursiv, astfel:
- Nivelul nodului radacina este 1;
- Nivelul oricarui nod diferit de nodul radacina este nivelul tatalui sau +1.
Observatie. Nivelul unui nod este 1+numarul de arce care alcatuiesc un "drum" de la nodul "radacina" la el. Exemplu: nodurile 3,4,7 au nivelul 3, nodurile 9 si 10 au nivelul 5.
Un subarbore B pentru arborele A este orice arbore care îndeplineste conditiile:
1. nodurile lui B sunt si noduri în A;
2. arcele lui B sunt si arce în A;
3. orice frunza din A care poate fi atinsa din radacina arborelui B trebuie sa apartina multimii nodurilor lui B.
Un tip de arbore special, cu aplicatii interesante în tehnicile de programare este arborele binar.
Arborele binar este arborele în care un nod are cel mult doi fii. În aceasta situatie se poate vorbi (pentru un arbore nevid) de cei doi subarbori (stâng si drept) ai unui arbore.
Reprezentarea în memorie a arborilor poate fi statica sau dinamica. În cazul static arborii se pot simula cu ajutorul tablourilor.
Datorita dinamismului structurilor modelate printr-un arbore, varianta de implementare dinamica este preferabila variantei statice. In acest caz, daca arborele este binar, o celula va contine trei câmpuri: un câmp pentru memorarea informatiei specifice nodului (informatia utila) si doua câmpuri care contin adresa radacinii subarborelui stâng, respectiv drept.
Operatiile fundamentale asupra arborilor includ: parcurgerea arborelui, stergerea, cautarea sau adaugarea unui nod. Doua tipuri de parcurgere a unui arbore sunt folosite frecvent: parcurgerea în latime si parcurgerea în înaltime.
In cazul parcugerii în latime se viziteaza si prelucreaza nodurile în ordinea: radacina, nodurile de la stânga spre dreapta de pe primul nivel, de pe al doilea nivel etc. Astfel, rezultatul parcurgerii în latime a arborelui din prima figura: 1, 2, 5, 6, 3, 4, 7, 8, 9, 10.
In cazul parcurgerii în adâncime trecerea de la un nod x la fratele sau y din dreapta se face numai dupa ce s-au vizitat si prelucrat toate nodurile descendente din x. Rezultatul parcurgerii în adâncime a arborelui din prima figura este urmatoarea: 1, 2, 3, 4, 5, 7, 8, 9, 10, 6.
Pentru parcurgerea in latime sau adancime (inaltime) putem utiliza algoritmul folosit la grafuri:
//PARCURGEREA IN LATIME A GRAFURILOR NEORIENTATE
//BREADTH FIRST (BF)
#include "graf.cpp"
int a[50][50],vizitat[50],lista[50],n,j,k,p,x,y;
void PBF(int i)
{
int x=lista[i];
for (y=1;y<=n;y++)
if ((a[x][y]==1)&&(vizitat[y]==0))
{
k++;
lista[k]=y;
vizitat[y]=1;
}
if (i<n) PBF(i+1);
}
main()
{
citire_graf("graf.in",a,n);
afisare_graf(a,n);
cout<<"Nodul de plecare pentru BF: ";cin>>p;
lista[1]=p;
vizitat[p]=1;
k=1;
PBF(1);
cout<<"Lista nodurilor:"<<endl;
for (k=1;k<=n;k++) cout<<lista[k]<<" ";
}
//PARCURGEREA IN ADANCIME A GRAFURILOR NEORIENTATE
//DEPTH FIRST (DF)
#include "graf.cpp"
int a[50][50],vizitat[50],lista[50],n,x,k;
void PDF(int x)
{
int y;
lista[k++]=x; vizitat[x]=1;
for (y=1;y<=n;y++)
if(a[x][y]==1 && vizitat[y]==0) PDF(y);
}
int main()
{
citire_graf("graf.in",a,n);
afisare_graf(a,n);
cout<<"Nodul de plecare pentru DF: ";cin>>x;
k=1;
PDF(x);
cout<<"Lista nodurilor:"<<endl;
for (k=1;k<=n;k++)
cout<<lista[k]<<" ";
}
Un graf conex si fara cicluri, sau conex si m=n-1, sau fara cicluri si m=n-1 (m-muchii, n-noduri), sau fara cicluri maximal, sau conex minimal, sau orice pereche de noduri legata de un lant si numai unul - se numeste arbore.
Arbore partial de cost minim - APM
Suma costurilor muchiilor unui graf se numeste costul grafului (c).
Pentru un graf G, conex, cu functia de cost c, exista un graf partial H conex si de cost minim, care este A.P.M.
Algoritmul lui Kruskal de determinare a APM:
1. se initializeaza lista L(k)=k adica se presupune ca fiecare nod apartine unei componente conexe distincte (se elimina toate muchiile)
2. se ordoneaza crescator muchiile dupa costurii
3. se selecteaza o muchie [p,q]: daca numarul de muchii=n-1; STOP – s-a obtinut un APM, daca nu :
4. se verifica daca nodurille muchiei selectate apartin aceleasi componente conexe: L(p)=L(q), daca da (s-ar obtine un ciclu) se selecteaza urmatoarea muchie iar daca nu:
5. se va selecta muchia [p,q] ca o noua muchie a APM. Daca L(p)<L(q) atunci toate elementele din componenta conexa q trec in p (sau invers).
Se merge la pasul 3.
In final toate nodurile apartin componentei conexe 1.
Arbori binari
Definitie: Numim arbore binar un arbore in care fiecare nod are zero, unul sau cel mult doi fii (descendenti).
Definitie: Un arbore binar cu proprietatea ca fiecare nod cu exceptia frunzelor (nodurilor terminale) are exact doi descendenti se numeste arbore binar complet.
Reprezentarea arborilor binari:
1. Metoda standard: Se specifică rădăcina RAD iar pentru fiecare nod se precizează desc. Stang S[i], descendentul drept D[i] (in caz ca exista) si informatia din nod (nr. Nodului). Lipsa unui descendent se simbolizeaza cu 0.Exemplu: Pentru arborele binar urmator:
RAD = 1
ST = { 2, 0, 5, 0, 6, 0, 0 }
DR = { 3, 0, 4, 0, 7, 0, 0 }.
2. Se folosesc vectorii TATA care precizeaza pentru fiecare nod i, nodul parinelui sau TATA[i] si DESC, vector care retine valorile –1 sau 1 In functie de nodul i care este fie descendent stâng, fie descendent drept.
TATA = { 0, 1, 1, 3, 3, 5, 5 }
DESC = { 0, -1, 1, 1, -1, -1, 1 }.
3. Reprezentarea cu paranteze:
- se scrie nodul radacina;
- ficare nod va fi urmat de: paranteza rotunda, descendent stang, virgula, descendent drept si paranteza rotunda inchisa
1 ( 2 , 3 ( 5 ( 6 , 7 ) , 4 ) ) sau
1 ( 2(0,0) , 3 ( 5 ( 6(0,0) , 7(0,0))) , 4(0,0)))
Pentru arborii binari, trei tipuri de parcurgere în adâncime sunt uzuale: parcurgerea în preordine (RSD), în inordine (SRD) si în postordine (SDR).
Prescurtarile au urmatoarea semnificatie:
RSD - Radacina, Stânga, Dreapta - se prelucreaza radacina, subarborele stâng, subarborele drept;
SRD - Stânga, Radacina, Dreapta - se prelucreaza subarborele stâng, radacina, subarborele drept;
SDR - Stânga, Dreapta, Radacina - se prelucreaza subarborele stâng, subarborele drept, radacina.
