GRAFURILE ORIENTATE
Definitie
Se numește graf orientat notat cu G o pereche ordonată de mulțimi {X,U} G= {X,U} unde X este mulțimea vârfurilor si U este multimea arcelor.
X={1,2,3,4,5}
U={(1,2),(1,3),(2,5),(4,2),(4,5)}
TERMINOLOGIE
Elementele mutimii U se numesc arce,iar multimea U se mai numeste si multimea arcelor.
Varfurile adiacente sunt orice pereche de varfuri care formeaza un arc.
Pentru arcul (x,y) spunem ca x este extremitate initiala iar y este extremitate finala.
Se numesc arce incidente doua arce care au o extremitate comuna.Se numeste succesor al varfului X orice varf in care ajunge un arc care pleaca din varful X.
Se numeste predecesor al varfului X orice varf in care intra un arc care pleaca din varful X.
Nod sursa al grafului este nodul care are multimea succesorilor formata din toate celelalte noduri mai putin el iar multimea predecesorilor sai este vida. Nod destinatie al grafului este nodul care are multimea predecesorilor formata din toate celelalte noduri mai putin el iar multimea succesorilor sai este vida.Se numeste nod terminal un nod care are suma gradelor egala cu 1.
Se numeste nod izolat un nod care are suma gradelor egala cu 0.
Elementele mutimii U se numesc arce,iar multimea U se mai numeste si multimea arcelor.
Varfurile adiacente sunt orice pereche de varfuri care formeaza un arc.
Pentru arcul (x,y) spunem ca x este extremitate initiala iar y este extremitate finala.
Se numesc arce incidente doua arce care au o extremitate comuna.Se numeste succesor al varfului X orice varf in care ajunge un arc care pleaca din varful X.
Se numeste predecesor al varfului X orice varf in care intra un arc care pleaca din varful X.
Nod sursa al grafului este nodul care are multimea succesorilor formata din toate celelalte noduri mai putin el iar multimea predecesorilor sai este vida. Nod destinatie al grafului este nodul care are multimea predecesorilor formata din toate celelalte noduri mai putin el iar multimea succesorilor sai este vida.Se numeste nod terminal un nod care are suma gradelor egala cu 1.
Se numeste nod izolat un nod care are suma gradelor egala cu 0.
GRADUL UNUI NOD
-grad extern este egal cu numarul arcelor care au extremitate initiala( numarul arcelor care ies din X)
-grad intern este egal cu numarul arcelor care au extremitate finala( numarul arcelor care intra in X)
-grad extern este egal cu numarul arcelor care au extremitate initiala( numarul arcelor care ies din X)
-grad intern este egal cu numarul arcelor care au extremitate finala( numarul arcelor care intra in X)
Se noteaza:
Un varf izolat este un varf care are gradul intern egal cu extern ,egal cu zero.
- Multimea (gama plus) si (gama minus)
-Multimea pentru varful x este egala cu multimea varfurilor care reprezinta succesorii varfului x.- Multimea reprezinta multimea varfurilor care sunt predecesoare varfului x.
-Multimea (omega plus) si (omega minus) -Multimea reprezinta multimea muchilor care au ca extremitate initiala varful x.Multimea reprezinta multimea muchilor care au ca extremitate finala varful x
Un nod terminal este un nod care are suma gradelor externe si interne egala cu 1.
Teoreme
2.Intr-un graf orientat cu n varfuri ,suma gradelor interne ale tuturor nodurilor este egala cu suma gradelor externe ale tuturor nodurilor si cu numarul de arce.
Suma gradelor interne ale tuturor varfurilor este egala cu suma gradelor externe si este egala cu numarul de arc
Lant,drum in grafurile orientate
Def :Numim lant intr-un graf orientat o succesiune de varfuri cu proprietatea ca oricare 2 varfuri consecutive sunt adiacente. 
5,1,2,4,3-lant elementar
5,1,2,4,3-lant elementar
3,4,2,5-lant elementar
3,4,2,5,1,2-lant neelementar
1,2,3-nu este lant
Numim drum o succesiune de noduri cu proprietatea ca intre oricare 2 varfuri succesive exista un arc.
5,1,2,4,3-nu este drum
3,4,2,5-nu este drum (deoarece intre 3 si 4 nu avem arc,doar intre 4 si 3)
2,1,4,3-drum elementar
Graf Conex
Un graf G se numeste conex daca intre oricare 2 varfuri diferite exista un lant care sa le uneasca.
Componenta conexa a unui graf orientat
Daca avem un graf G care nu este conex,se numeste componenta conexa a grafului G un subgraf al sau care este conex.
Obs :Un graf conex are o singura componenta conexa.
Graful are 2 componente conexe.
Graf tare conex
Def :Un graf orientat G se numeste tare conex daca indeplineste urmatoarea proprietate :pentru oricare 2 varfuri x,y(x !=y) exista drum de la varful x la varful y si un alt drum de la varful y la varful x.
Daca un graf orientat G nu este tare conex se numeste componenta tare conexa a grafului un subgraf tare conex al sau.
GT1 GT2
GT1-este un graf conex
Componenta tare conexa :{1,3,7},{4,5},{2},{6}
GT2-este un graf tare conex
GT4
GT4-graful nu este conex
Componentele conexe sunt formate din submultimile ;{1,2},{3,4,5,8},{6,7,9}
Teoreme
1.Daca un graf nu contine un lant intre 2 noduri x si y atunci contine un lant elementar intre nodurile x si y.
2.Daca un graf contine un drum intre 2 noduri x si y atunci contine un drum elementar intre nodurile x si y.
3.Daca un graf contine un ciclu atunci contine si un ciclu elementar.
4.Daca un graf contine un circuit atunci contine si un circuit elementar.
Teoreme :
1.Numarul minim de muchii necesare ca pentru un graf neorientat sa fie conex este n-1.
2.Un graf conex cu n noduri si n-1 muchii este aciclic si maximal cu aceasta proprietate.
3.Daca un graf neorientat conex are n noduri si m muchii ,numarul de muchii care trebuie eliminate pentru a obtine un graf partial conex aciclic este m-n+1.
4.Daca un graf are n noduri,m muchii si p componente conexe, numarul de muchii care trebuie eliminate pentru a obtine un graf partial aciclic(arbore) este egal cu m-n+p.
5.Pentru a obtine dintr-un graf neorientat conex 2 componente conexe,numarul minim de muchii care trebuie eliminate este cel mult egal cu gradul minim din graf.
6.Numarul maxim de muchii dintr-un graf neorientat cu n noduri si p componente conexe este (n-p)*(n-p+1)/2.
DEFINITIE. Se numeşte graf ponderat un graf orientat sau nu în care fiecărei muchii i s-a asociat un cost dat, de obicei, o funcţie de cost f: U→R. Exemplu de graf ponderat:
DEFINITIE. Graful orientat G1=(X,U1) se numeşte graful transpus al grafului G dacă G1 se obţine din graful G prin inversarea sensului arcelor sale.
REPREZENTAREA GRAFURILOR ORIENTATE
Matricea de incidenţă
Matricea de incidenţă este o matrice cu n linii şi m coloane. Pe fiecare coloană vom avea o valoare de 1 care corespunde extremităţii iniţiale a unui arc, o valoare de -1 care corespunde extremităţii finale a unui arc, toate celelalte fiind 0.
Lista arcelor
Este formată din m elemente care conţin fiecare, câte o pereche de noduri, x şi y care formează un arc.
Lista vecinilor În lista vecinilor pentru fiecare nod se specifică succesorii.
PARCURGEREA GRAFURILOR ORIENTATE IN ADANCIME
Parcurgerea unui graf in adancime se face prin utilizarea stivei (alocate implicit prin subprograme recursive).
Pentru fiecare varf se parcurge primul dintre vecinii lui neparcursi inca
Dupa vizitarea varfului initial x1, se exploreaza primul varf adiacent lui, fie acesta x2 , se trece apoi la primul varf adiacent cu x2 si care nu a fost parcurs inca , s.a.m.d.
Fiecare varf se parcurge cel mult odata
De exemplul pentru garful din figura de mai jos, se va proceda in felul urmator:
se porneste din varful 1, (se poate incepe de la oricare alt varf)
se exploreaza in continuare primul vecin al acestuia acestuia : varful 2,
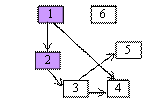se obtine 1,2
dupa care din 2 se exploreaza varful adiacent cu acesta si care nu a fost vizitat : 3.
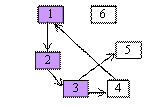se obtine 1,2,3
In continuare ar trebui sa se parcurga vecinul lui 3 nevizitat : 4
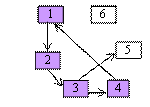se obtine 1, 2, 3, 4
Pentru varful 4 ar trebui sa se parcurga primul sau vecin neparcurs (varful 1 dar acesta a fost deja parcurs. Nu mai avem ce vizita si se trece la nivelul anterior din stiva, la varful 3 :
1, 2, 3, 4 Se parcurge vecinul sau nevizitat, varful 5 .
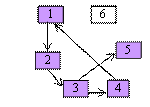
Se obtine : 1, 2, 3, 4 , 5.
Varful 3 nu mai are vecini nevizitati si se trece pe nivelul anterior din stiva, varful 2 : 1, 2, 3, 4 , 5. Nici acesta nu mai are vecini nevizitati si se trece pe nivelul anterior la varful 1 : 1, 2, 3, 4 , 5. Cum nici acesta nu mai are vecini nevizitati se incheie algoritmul.
Niciun comentariu:
Trimiteți un comentariu