Grafuri neorientate

GRAFURILE NEORIENTATE

Definiţie

Se numeşte graf neorientat G=(X,U) o pereche de mulţimi (X,U), unde X este o mulţime finită şi nevidă de elemente numite noduri (vârfuri) iar U o mulţime de perechi, formate cu elemente distincte din mulţimea X numite muchii.

Se numesc noduri adiacente orice pereche de noduri între care există o muchie.

ex:muchia (1,2)

Spunem că un nod este incident cu o muchie daca nodul reprezintă o extremitate pentru aceea muchie.

ex:nodul 1 este incident cu muchia (1,2)

Spunem ca 2 muchii sunt incidente daca au un nod comun .

ex: muchia (1,2), (1,3) au nodul 1 comun

Nodurile vecine unui nod sunt toate noduriile adiacente cu nodul respectiv.

Gradul unui nod X al grafului G este egal cu numarul de muchii incidente cu nodul respectiv şi se noteaza cu d(x).

ex:d(3)=5

Un nod care are gradul 1 se numeşte nod terminal.

ex: d(4)=1

Un nod care are gradul 0 se numeşte vârf izolat.

ex: d(7)=0

REPREZENTAREA GRAFURILOR NEORIENTATE

MATRICEA DE ADIACENTA

DEFINITIE 

           Fie G=(V,M) un graf neorientat, cu n varfuri si m muchii. Matricea de adiacenta asociata grafului G este o matrice patratica de ordinul n, cu n elemente, definite astfel:

i,j={ 1, daca [i,j] apartine M

                                        0, daca [i,j] nu apartine M

 EXEMPLU

REPREZENTARE GRAFICA	MATRICEA A	MATRICE DE ADIACENTA
	a11    a12    a13     a14          a21    a22    a23      a24 A=     a31    a32    a33      a34          a41    a42    a43      a44	0    0    1   1          0    0    1   1          1    1    0   0          1    1    0   0

PROPRIETATI

• matricea de adiacenta este o mnatrice patratica de ordinul n, si simetrica fata de diagonala principala;
• matricea de adiacenta are toate elementele, de pe diagonala principala, egale cu zero;
• numarul elementelor egale cu 1 de pe linia i(sau coloana j) este egal cu gradul varfului i;
• daca varful i este izolat pe linia i (sau coloana j) nu sunt elemente egale cu 1.

 IMPLEMENTAREA MATRICII DE ADIACENTA

#include<iostream.h>

void main()

 {
int m,n,x,y,i,j, a[20][20];
 cout<<" noduri n=";  cin>>n;
 cout<<"muchii m="; cin>>m;
 for(i=1;i<=m;i++)
 {    cout<<"x=";cin>>x;
       cout<<"y=";cin>>y;
       a[x][y]=1; a[y][x]=1;      }
 cout<<"matricea de adiacenta este="<<endl;
 for (i=1;i<=n;i++) 

{

for(j=1;j<=n;j++)

cout<<a[i][j]<<" ";

cout<<endl;}

LISTA DE ADIACENTA

Fie G=(V, M) un graf neorientat cu n vârfuri (V={1,2, ..., n}) si m muchii.
                Reprezentarea grafului G prin liste de adiacență constă în:
- precizarea numărului de vârfuri, n;
- pentru fiecare vârf i, se precizează lista i a vecinilor săi, adică lista nodurilor adiacente cu nodul i.

Fie graful din figura urmatoare:

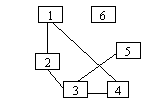
Lista vecinilor nodului 3: 2, 4, 5 (noduri adiacente)

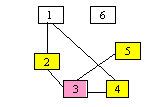
Nodul 6 nu are vecini (este izolat)

Pentru intreg graful vom avea mai multe liste :

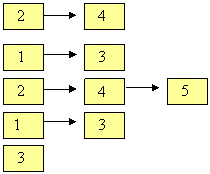Nodul 1 :

Nodul 2 :

Nodul 3 :

Nodul 4 :

Nodul 5 :

  Implementarea în limbajul C++, a ideii prezentate mai sus, se realizează conform secvenței de program :

int L[20][20];
int nr_vec[20];
cout<<"n=”; cin>>n;
for (i=1;i<=n;i++)
{cout<<"Dați numărul veciniior nodului "<<i; cin>>nr_vec[i];
for (j=1;j<=nr_vec[i];j++)
cin>>L[i][j];}

GRAFURI SPECIALE

Numim lanţ o succesiune de noduri cu proprietatea că oricare ar fi 2 noduri successive ele sunt adiacente.

Se numeşte ciclu ,un lanţ în care toate muchiile sunt distincte 2 câte 2 şi între primul şi ultimul nod există o muchie.

Se numeşte lungimea unui lanţ ,numărul de muchii din care este format.

Se numeşte lanţ elementar,un lanţ care conţine doar noduri distincte.

Se numeşte lanţ simplu,un lanţ care conţine doar muchii distincte.

Graful G se numeşte nul dacă mulţimea U este vidă (nu are muchii).
Un graf se numeşte complet dacă are proprietatea că oricare 2 noduri ale sale sunt adiacente.
Teoremă: Numărul de muchii ale unui graf complet cu n noduri este
[n(n-1)]/2.
Se numeşte graf parţial al lui G=(X,U) graful Gp=(X,V) unde V este egal sau inclus în U (din graful G eliminăm muchii).
Se numeşte subgraf al lui G=(X,U), Gs=(Y,V) unde Y este egal sau inclus în X şi toate muchiile din mulţimea V aparţin şi mulţimii U,care au ambele extremităţi în mulţimea Y,adică se obţine din graful G prin eliminarea unor noduri şi a tuturor muchilor incidente cu acestea.
Se numeşte graf complementar al lui G,graful Gc care are propritatea că 2 noduri sunt adiacente în graful complementar dacă şi numai dacă nu sunt adiacente în graful G.
Teoremă: Numărul grafurilor parţiale ale unui graf cu m muchii este 2 la puterea m.
Teoremă: Numărul de subgrafuri ale unui graf cu n noduri este 2ⁿ-1.
Conexitate
Definitie:

1) Un graf G se numeşte graf conex dacă are proprietatea că pentru orice pereche de noduri distincte există un lanţ care le leagă.
2) Dacă un graf G nu este conex se numeşte componentă conexă a grafului, un subgraf conex
al său maximal în raport cu această proprietate (conţine numărul maxim de noduri din graful G care au proprietatea că sunt legate de un lanţ).

Teoreme:
1) Numărul minim de muchii necesare pentru ca un graf neorientat să fie conex este: n-1,unde n reprezintă numărul de noduri.
2) Un graf conex cu n noduri şi n-1 muchii este aciclic şi maximal în raport cu această proprietate.
3) Dacă un graf neorientat conex are n noduri şi m muchii, numărul de muchii care trebuie eliminate pentru a obţine un graf parţial conex aciclic este: m-n+1.
4) Dacă un graf are n noduri şi m muchii şi p componente conexe, numărul de muchii care trebuie eliminat pentru a obţine un graf parţial aciclic(arbore) este egal cu: m-n+p.
5) Pentru a obţine dintr-un graf neorientat conex 2 componente conexe numărul minim de muchii care trebuie eliminate este egal cu gradul minim din graf.
6) Numărul maxim de muchii dintr-un graf cu n noduri şi p componente conexe este [(n-p)(n-p+1)]/2.
Grafuri speciale

Un graf G se numeşte graf bipartit dacă există două mulţimi nevide de noduri A si B care au proprietatea: A ∩ B= Ø iar A U B=X şi orice muchie din mulţimea U are o extremitate în mulţimea A şi o altă extremitate în mulţimea B.
Un graf bipartit se numeşte graf bipartit complet dacă pentru oricare nod X care aparţine mulţimii A şi orice nod Y care aparţine mulţimii B există o muchie care le leagă.

Se numeşte lanţ Hamiltonian,lanţul care conţine toate nodurile grafului şi este elementar.
Un graf care conţine un ciclu Hamiltonian se numeşte graf Hamiltonian.
Un ciclu se numeşte eulerian,ciclul elementar ce conţine toate muchiile grafului.
Se numeşte graf eulerian,graful care conţine un ciclu eulerian.

TEOREME

1) Un graf cu mai mult de 2 noduri este Hamiltonian dacă graful fiecărui nod este mai mare sau egal decât n/2.
2) Un graf ce nu conţine vârfuri izolate este eulerian dacă şi numai dacă este conex iar gradele tuturor noduriilor sunt numere pare.
3) Numărul de cicluri hamiltoniene dintr-un graf complet cu n noduri este (n-1)!/2.

PARCURGEREA GRAFURILOR NEORIENTATE

Prin parcurgerea unui graf se întelege "vizitarea" vârfurilor sale într-o anumita ordine, data de un anumit criteriu.

Exista doi algoritmi de parcurgere  a grafurilor neorientate:

Ø      algoritmul de parcurgere în latime BF;

Ø      algoritmul de parcurgere în adîncime DF.

1.     Algoritmul de parcurgere în latime BF

1.     Algoritmul de parcurgere în latime BF

Se porneste de la un vârf de start care se viziteaza, apoi se viziteaza toti vecinii lui. Pentru fiecare dintre aceste vârfuri, se viziteaza vecinii lui care nu au fost înca vizitati. Pentru noile vârfuri se procedeaza la fel: se viziteaza vecinii acestora care nu au fost înca vizitati. Procedeul continua pâna când s-au vizitat toate vârfurile.

                                          

Figura 9.

Exemplu:

Fie graful G=(X,U) din figura 9. presupunem ca vârful de start este 1.

Pasii parcurgerii	Noduri vizitate
·      Vizitam mai întâi vârful de start unu;	1
·      Vizitam apoi vecinii lui 1, care sunt 2, 5 si 6	2, 5, 6
·      Pentru fiecare dintre acesti vecini ai lui 1, vizitam si vecinii sai nevizitati înca: -  vecinii lui 2 sunt 1, 3 si 4, dar nevizitati sunt decât 3 si 4 -  vecinii lui 5 sunt 1, 2 si 7, dar nevizitat este numai 7 -  vârful 6 nu mai are vecini nevizitati
	3,4
	7
·      Am vizitat pâna acum vecinii vârfurilor 1,2,5 si 6. Mai trebuie vizitati vecinii noilor vârfuri vizitate la pasul anterior, si anume vecinii vârfurilor 3,4 si 7. Dar observam ca vârfurile 3,4 si 7 nu mai au vecini nevizitati.deci parcurgerea se încheie.

  Ordinea vizitarii în parcurgerea BF este 1, 2, 5, 6, 3, 4, 7.

2.     Algoritmul de parcurgere în latime BF

Metoda este urmatoarea: alegem vârful de pornire, pentru acesta se alege primul vecin al sau nevizitat înca, pentru acest vecin cautam primul vecin al sau nevizitat si asa în continuare. În cazul în care un vârf nu mai are vecini nevizitati atunci ne întoarcem la nodul anterior, iar pentru acel nod cautam urmatorul vecin nevizitat al sau.

Pentru graful de mai sus, din fig 9,parcurgerea în adâncime plecând de la vârful 1 este: 1,2,3,4,6,7,5.